방송통신대학교 알고리즘 강의 정리 자료입니다.
1. 과목소개




컴퓨터 과학 = 컴퓨터 + 데이터 + 프로그램 + 알고리즘
컴퓨터의 한계는 프로그램 존재 여부에 따라 정해지며, 프로그램의 존재 여부는 문제를 푸는 방법인 알고리즘과 연계되게 됨. 즉, 컴퓨터 과학은 알고리즘 과학이라고도 할 수 있음.
2. 기본 개념
컴퓨터 과학이란?
: 컴퓨터를 활용해서 주어진 문제를 해결하기 위한 학문임.

알고리즘이란?
: 문제해결을 위한 "레시피(Recipe)"로 단계적인 조리절차를 따르면 음식을 만들 수 있듯이 알고리즘의 단계적인 처리 절차를 따르면 주어진 답을 구할 수 있음. 레시피의 목표가 맛있고 몸에 좋은 음식과 같은 것이 있듯이 알고리즘도 효율적인 알고리즘을 만드는 것을 목표로 함.


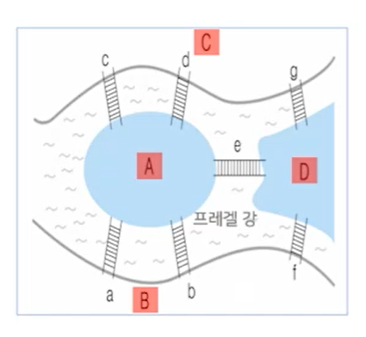
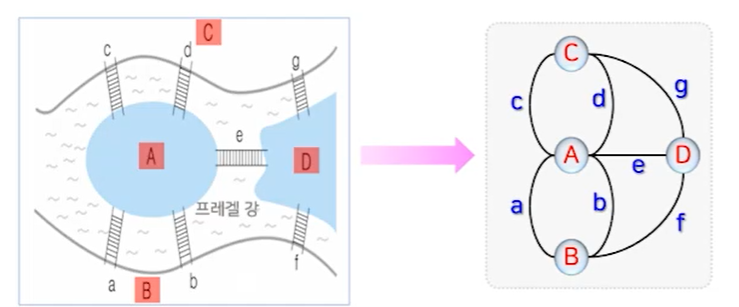
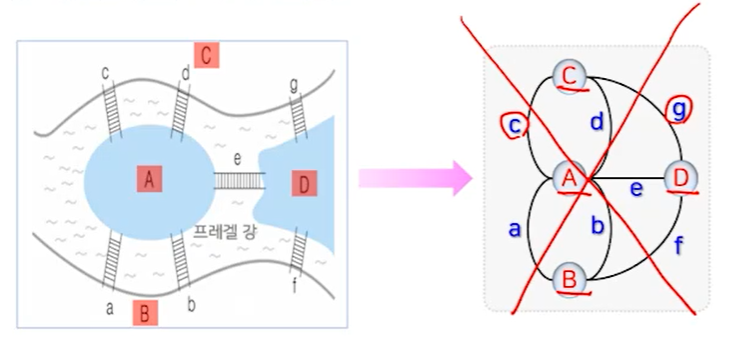
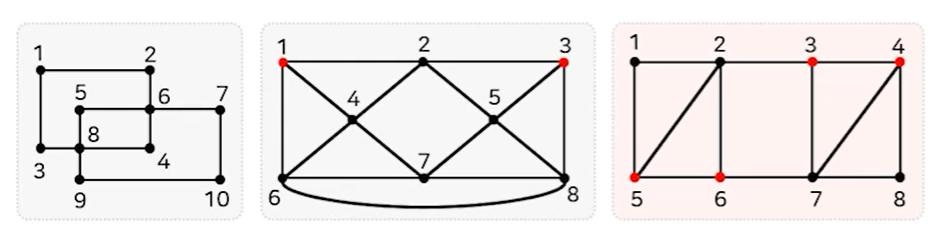
오일러 경로(그래프의 모든 간선을 오직 한 번씩만 지나가는 경로)를 찾는 문제
: 퀘닉스버그 다리문제에서 유래됨. 4개의 섬과 7개의 다리가 있는 경우 다리를 오직 한 번씩만 지나면서 원래대로 돌아올 수 있는지를 찾는 문제로 그래프로 모델링할 수 있음.

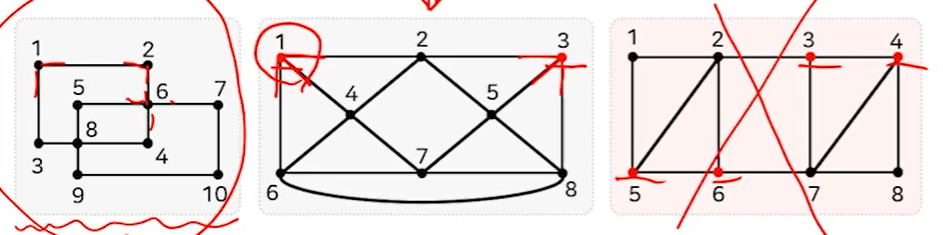
최단 경로를 찾는 문제
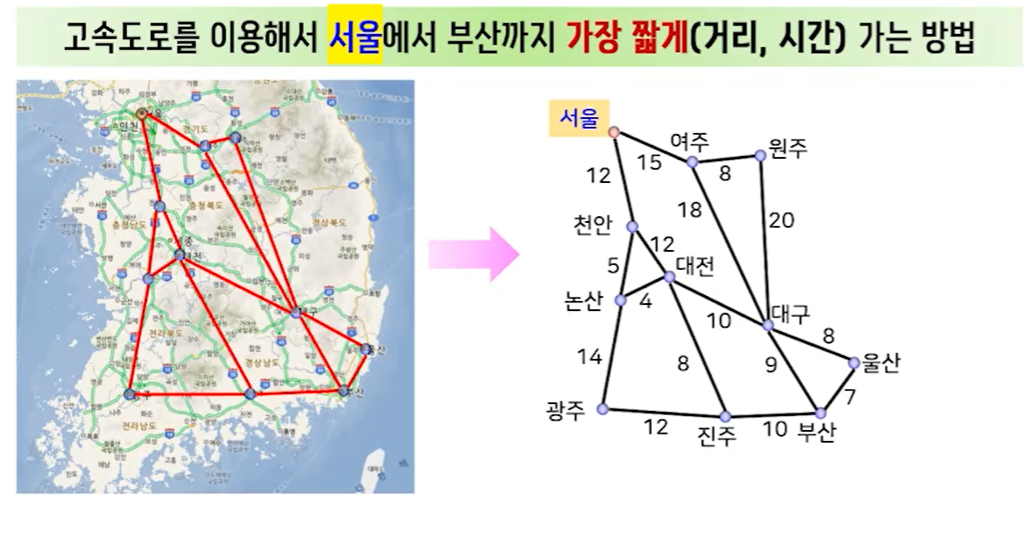
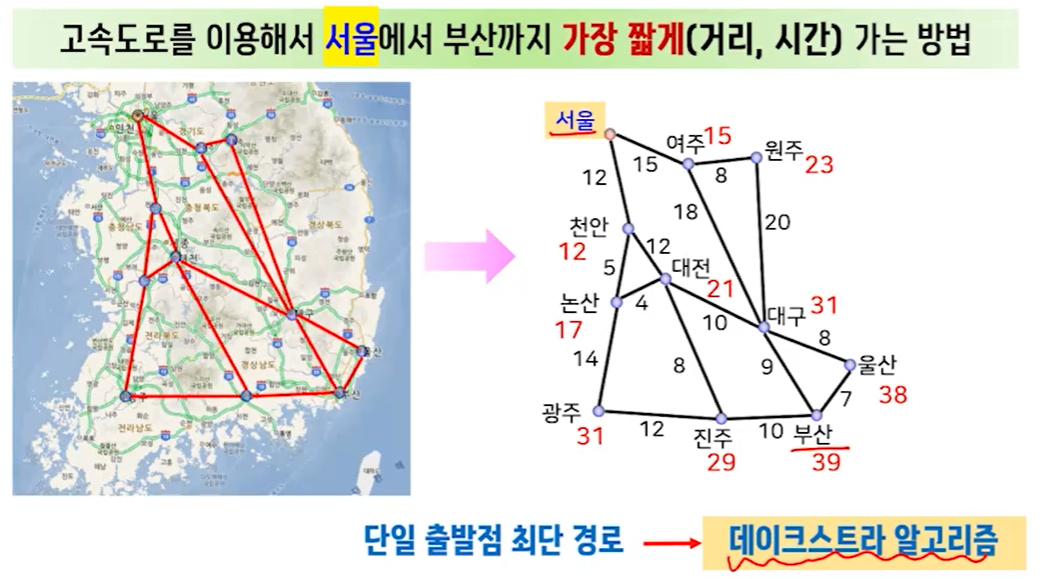
결국 알고리즘이란 주어진 문제를 해결하거나 함수를 계산하기 위해 따라야할 명령어들을 단계적으로 나열한 것이며, 4가지 조건이 따라오게 됨.
- 입출력
: 0개 이상의 외부 입력과 1개 이상의 출력을 생성해야함.
- 명확성
: 각 명령은 모호하지 않고 단순 명확해야함.
- 유한성
: 한정된 수의 단계를 거친 후에는 반드시 종료해야함.
- 유효성
: 모든 명령은 컴퓨터에서 수행할 수 있어야 함.
→ 주어진 문제에 대한 하나 이상의 결과를 생성하기 위해 모호하지 않고 단순 명확하며 컴퓨터가 수행할 수 있는 유한개의 일련의 명령어들을 순서에 따라 구성한 것
단, 문제를 해결할 수 있다고 하더라도 시간이 너무 오래 걸리거나 자원을 너무 많이 소모하는 것에 비해 결과물이 부합하지 않다면 적합하지 않음.(효율성의 문제)
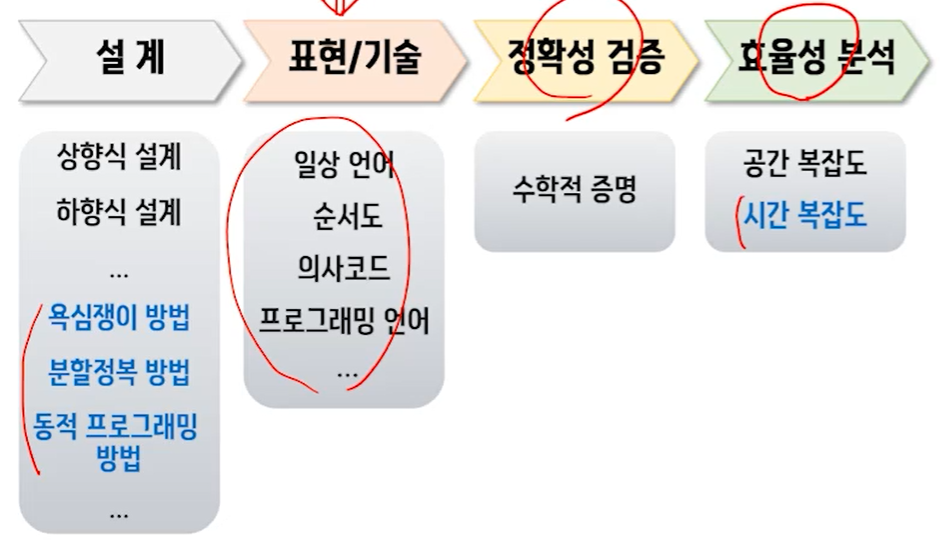

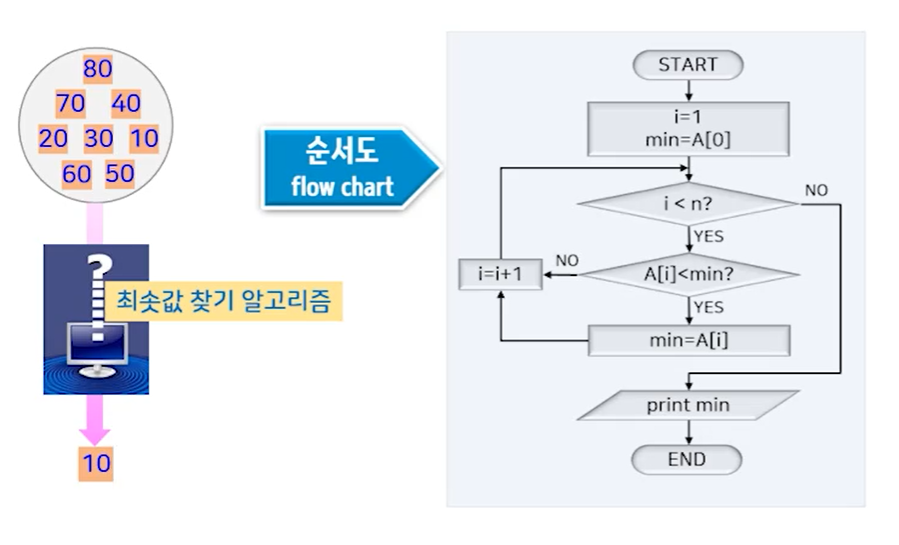
3. 알고리즘 설계
최솟값 찾기 문제
: 첫번째 방법과 두번째 방법은 둘 다 N-1번 비교를 해야하기에 효율성에서는 큰 차이가 없음.
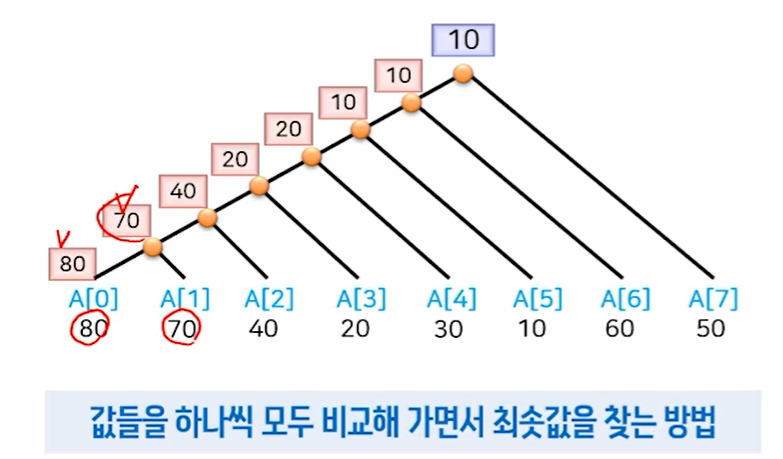
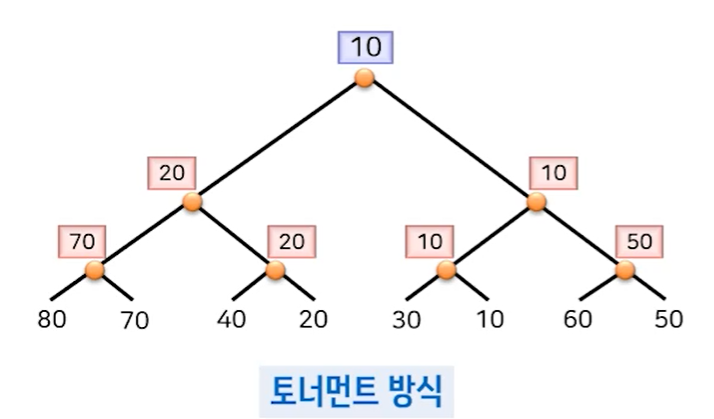
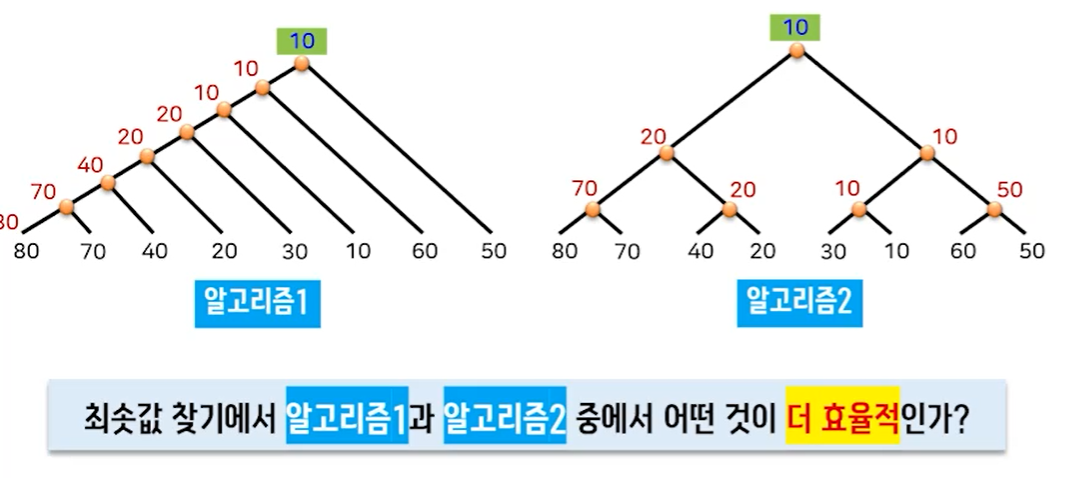
탐색 알고리즘
: 뒤섞인 카드에서 10을 찾는 경우
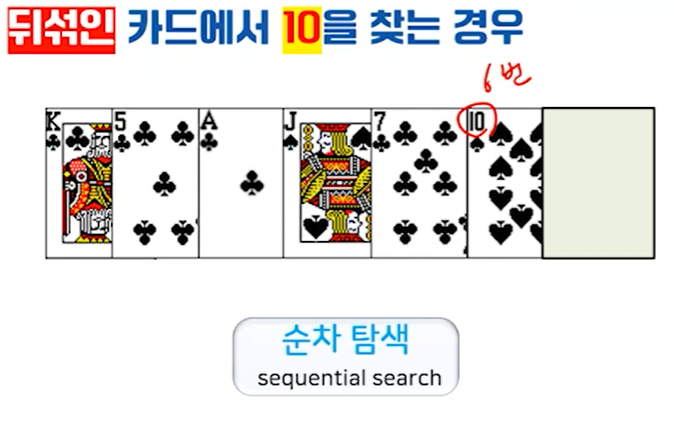

순서대로 나열된 카드 중에서 10을 찾는 경우

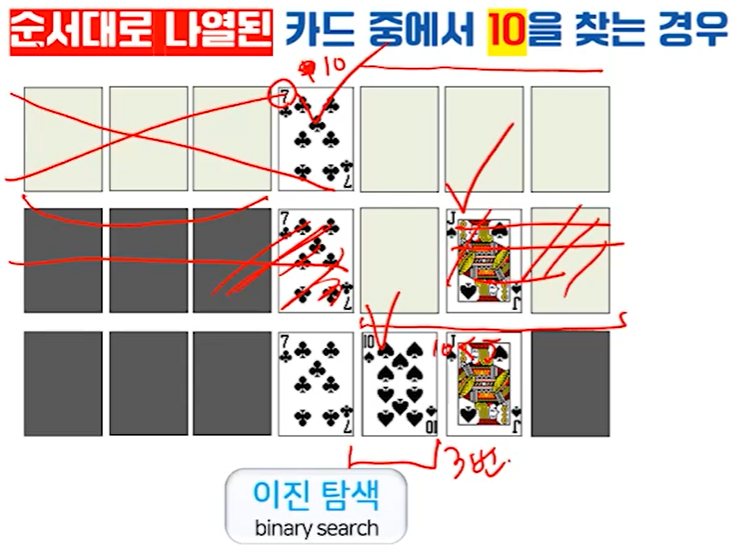

단순히 보기에는 이진탐색이 순차탐색보다 효율적으로 보일 수 있지만, 이진 탐색이 적용가능한 경우는 정렬이 되어 있는 경우에만 적용 가능하기에 속단할 수 없음. 즉, 효율성은 주어진 문제와 조건등에 따라 달라질 수 있으며 이에 따라 일반적/범용적인 설계 기법은 존재하지 않음.
대표적인 알고리즘 설계 기법으로는 욕심쟁이(greedy), 분할정복(divide-and-conquer), 동적 프로그래밍(dynamic programming)이 있음.
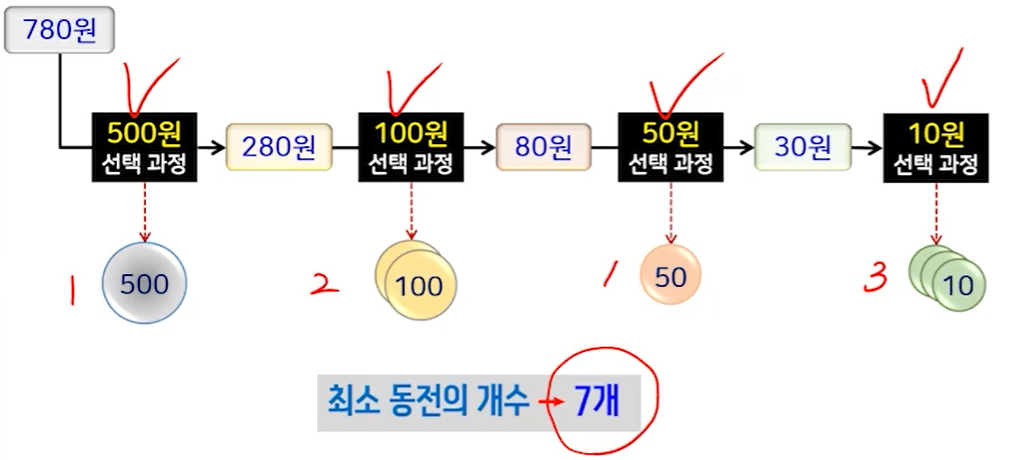
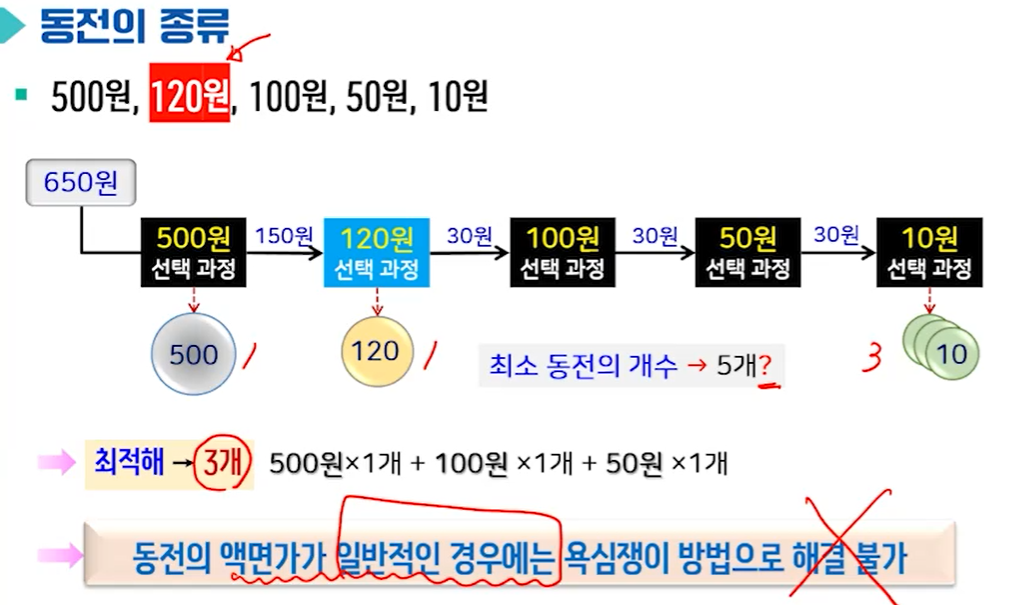
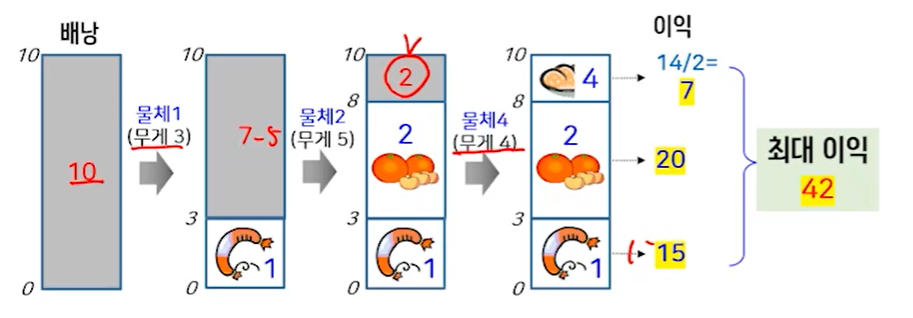
- 욕심쟁이방법, 탐욕적 방법, 탐욕 알고리즘, 그리디 알고리즘
: 해를 구하는 일련의 선택 과정에서 전후 단계의 선택과는 상관없이 각 단계마다 '가장 최선'이라 여겨지는 국부적인 최적해를 선택해 나가면 결과적으로 전체적인 최적해를 구할 수 있을 것이라는 희망적인(각 단계마다 선택한 국부적인 최적해가 항상 전체적인 최적해를 만들지 못할 수도 있음.) 전략을 취하는 방법으로 간단하면서도 효율적인 알고리즘을 만들 수 있는 강력한 기법임.









- 분할정복 방법
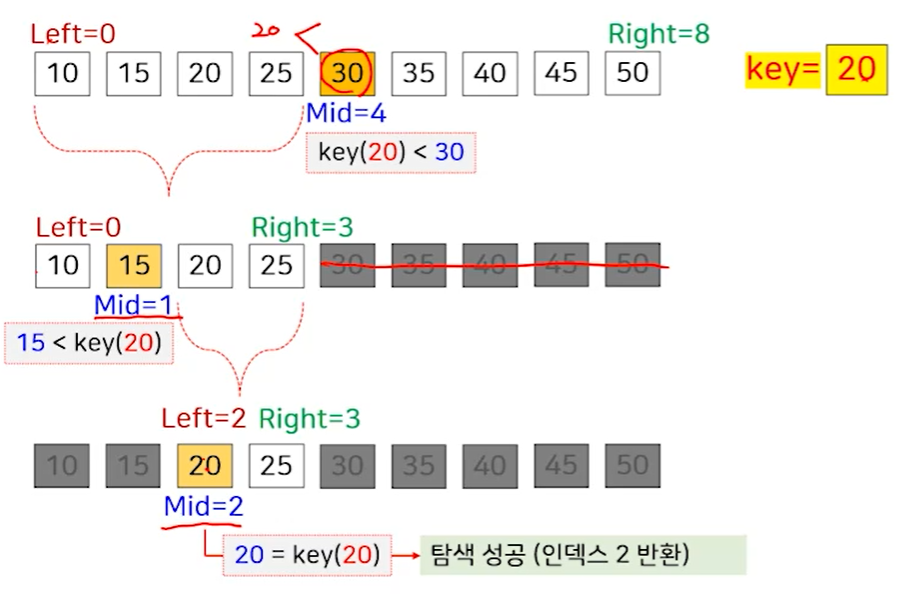
: 순환적으로 문제를 푸는 하향식(top-down) 접근 방법으로 주어진 문제의 입력을 더 이상 나눌 수 없을 때까지 2개 이상의 작은 문제들로 순환적으로 분할하고, 분할된 작은 문제들을 각각 해결한 후, 이들의 해를 결합하여 원래 문제의 해를 구하는 방식임. 분할된 작은 문제는 원래 문제와 동일하며 입력의 크기만 작아진다는 특징과 분할된 문제는 서로 독립적이기에 순환적인 분할 및 결과의 결합이 가능하다는 특징을 가짐. 각 순환 호출마다 세 단계의 작업을 수행함. 대표적인 적용 문제로 퀵 정렬, 합병 정렬, 이진 탐색 등이 있음.


- 동적 프로그래밍 방법
: 입력의 크기가 가장 작은 부분 문제부터 해를 구하여 테이블에 저장해놓고, 이를 이용해서 입력 크기가 보다 큰 문제의 해를 점진적으로 만들어가는 상향식(bottom-up)접근 방법임. 각각의 작은 문제는 원래 문제와 동일하고 입력의 크기만 작다는 점에서 분할정복과 유사하나 작은 문제들은 서로 독립일 필요가 없다는 차이가 있음. 대표적인 문제로 모든 정점 쌍 간의 최단 경로를 구하는 플로이드 알고리즘이 있음.
'방송통신대학교 > 3학년 1학기' 카테고리의 다른 글
| [인공지능] 1강. 인공지능의 개요 (1) | 2025.04.01 |
|---|---|
| [알고리즘] 2강. 알고리즘 소개 (2) (0) | 2025.04.01 |
| [데이터베이스 시스템] 5강. SQL (2) (0) | 2025.03.25 |
| [운영체제] 5강. 병행 프로세스 II (0) | 2025.03.20 |
| [운영체제] 4강. 병행 프로세스 I (0) | 2025.03.19 |




댓글