방송통신대학교 디지털논리회로 강의 정리 자료입니다.
1. 컴퓨터와 디지털 논리회로
시스템의 정의
: 목적을 위해 상호작용하는 매개체들의 집합

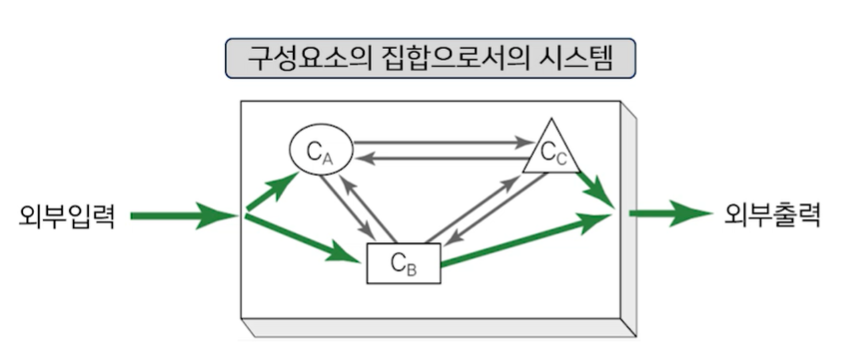
데이터의 표현 방법



디지털 시스템의 장점
- 편리성
: 데이터가 숫자로 바로 입출력
- 융통성
: 외부 조건의 변화에 따라 실행 순서 조절이 가능
- 단순성
: 0, 1이라는 두 가지 상태의 신호만 취급
- 안정성
: 0, 1이라는 두 가지 상태 신호만 유지하면 됨.
- 견고성
: 0, 1이라는 상태로 전송되어 신호가 왜곡되어도 잡음에 강함.
- 정확성
: 신호를 이산신호로 변환하여 처리
디지털 시스템을 만드는 단계


디지털 논리회로란?
: 2진 디지털 논리를 논리 게이트(Logic gate)로 구현한 것으로 하나 이상의 논리 게이트가 결합된 것이 논리회로임. 디지털 시스템을 구현하는 기본 요소이고, 디지털 시스템의 논리 설계 단계에서 설계됨.
디지털 논리회로는 저장요소가 없으면 가산기, 디코더 같은 조합논리회로로 저장요소가 있으면 레지스터, 카운터 같은 순서논리회로로 분류함.
컴퓨터의 구성
: 컴퓨터는 전자식 데이터 처리 시스템(Electronic Data Processing System)임.


집적회로(IC: Integrated Circuits)란?
: 디지털 회로의 구성요소로 디지털 게이트의 기능을 수행하는 전자 소자를 포함한 실리콘 반도체 크리스탈(silicon semiconductor crystal), 칩(Chip)이라고 함. 내부에 여러 게이트들이 목적에 부합하도록 상호 연결되어 있음.

집적도(level of integration)
: 실리콘 칩의 단위 면적당 집적할 수 있는 전자 소자(gate)의 수


디지털 논리계열(Digital Logic Families)
: 디지털 논리회로 설계에 사용되는 논리 소자의 집합으로 논리 게이트를 구현하기 위한 반도체 기술이나 전압, 전류 특성에 따라 분류됨. 각 논리계열의 기본적인 회로는 NAND gate, NOR gate, 인버터가 있음.

양논리와 음논리
: 게이트의 입력과 출력에서 2진 신호는 두 값 중에 한 값을 가짐. 두 논리 값 0과 1에 대한 두 신호 값 H(High: 높은 값), L(Low-낮은 값)을 할당하는 방법. 논리(1: 참, 0: 거짓)를 어떻게 정의하느냐에 따라 분류

2. 데이터 표현
수치 데이터
: 수를 특정 기수(base)를 기반으로 숫자의 조합으로 표현하는 체계로, 기수(base)는 진법에서 자리 값의 기준이 되는 값, 한 자리에서 표현할 수 있는 숫자의 총 개수를 의미함.(기수는 2 이상의 양의 정수) 숫자의 위치에 따라 각 숫자가 해당 자리의 값(가중치)을 결정하고, 가중치는 기수의 승수(거듭제곱)으로 계산됨.

r진법
: 기수가 r(r>=2)인 경우 r진법이라고 하며, r진법으로 표현된 수를 r진수라고 하고, 각 자리는 r개의 숫자(0~r-1)로 표현함. r진수 오른쪽 아래에 기수 r을 표기함.



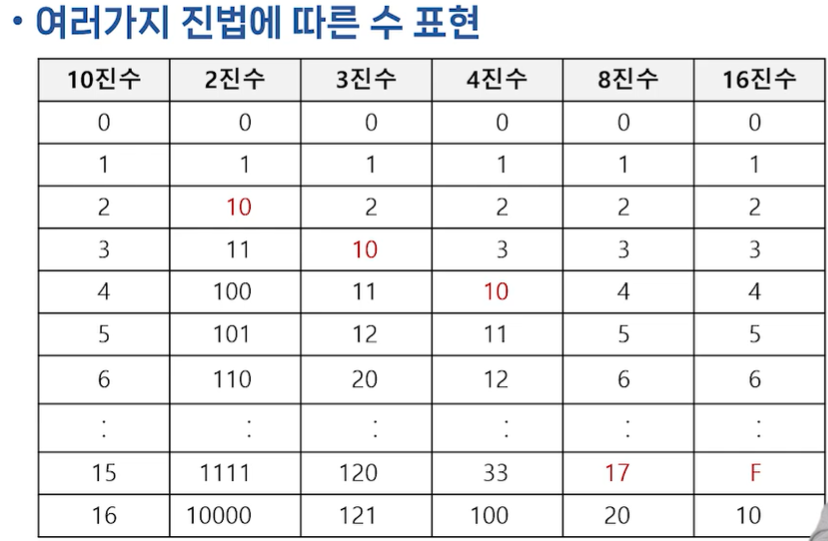
진수 변환
: 진법 체계의 공통 기반을 기준으로 변환이 가능함.





기타 변환
: 5진수를 8진수로 바꾸거나 2진수를 7진수로 바꾸려면 10진수로 변환한 후 해당 진수로 변환해야함. 몇몇 진수는 서로 직접적인 비트 그룹화 관계가 없음.(홀수 진수에서 짝수 진수로의 변환, 또는 그 반대 / 6진수를 4진수로 변환하는 등의 공통 기반 진수의 거듭제곱과 관계가 없을때)따라서 모든 진법의 공통기반인 10진수를 중간 변환으로 사용함.
컴퓨터에서의 대표적인 진법
- 2진수(Binary)
: 전기 신호의 ON/OFF를 기반으로 표현되는 가장 기본적인 숫자 체계
- 8진수(Octal)
: 2진수를 더 간결하게 표현하기 위해 사용되고, 현재는 사용 빈도가 낮음. 리눅스 OS에서 파일 권한 정보를 3비트로 표현하며 8진수로 요약됨.
- 16진수(Hexadecimal)
: 헥사코드(Hexa Code)이고, 메모리 주소, 색상 코드 등 현대 컴퓨터에서 널리 사용됨.
산술연산


보수(complement - 보충을 해주는 수)
: 주어진 숫자가 특정 기준 값에서 얼마나 떨어져 있는지를 나타내는 값으로 10진수 7에 대한 10의 보수는 3임. 기수가 r인 수 체계에서는 진보수은 r의 보수와 (r-1)의 보수가 존재하는데, 10진수에서는 진 보수 10의 보수와 r-1의 보수인 9의 보수가 있고, 2진수의 경우 진 보수인 2의 보수와 r-1의 보수인 1의 보수가 있음.
r의 보수와 r-1의 보수



2진수의 보수
: 보수는 주어진 숫자가 특정 기준 값에서 얼마나 떨어져 있는지를 나타내는 값으로 2진수에서 1의 보수는 주어진 값의 자리 수에서 표현할 수 있는 가장 큰 숫자를 기준 값으로 사용함.(2진수 10010에 대한 1의 보수에서 기준 값은 11111이 됨. 10010의 1의 보수는 기준 값 11111과 얼마나 떨어져 있는지를 나타내는 값임.)

보수를 이용한 감산



정수의 표현 방법

디지털 코드
- 10진수를 나타내는 2진 코드
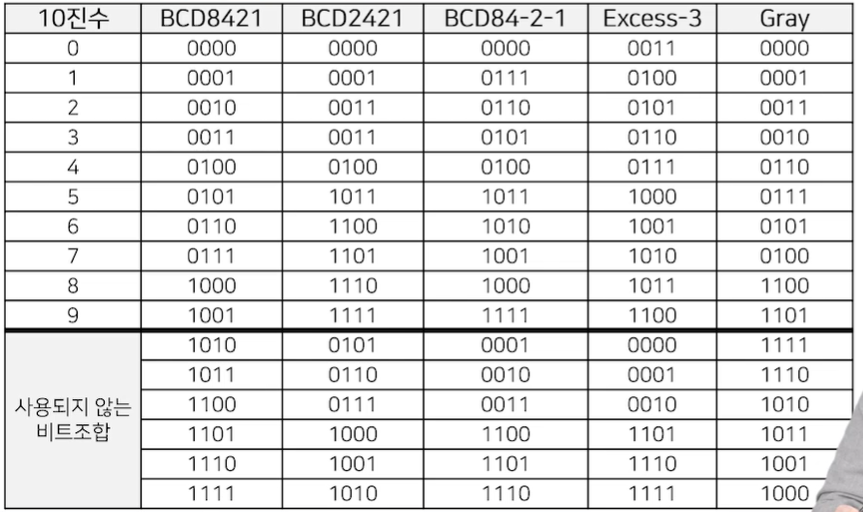
- 영 숫자 코드

댓글